引言:问题所在 —— 笨拙的厨师 (DFT)
想象一下,你是一位厨师,接到一份包含1024道菜的超级大订单。这份菜单就是我们的离散傅里叶变换 (DFT)。DFT的“蛮力”做法:这位厨师非常实在,但有点笨。他做每一道菜(计算一个频点 `X[k]`),都会从头开始,重新去菜市场买菜、洗菜、切菜(遍历所有 `N` 个输入点 `x[n]` 并做乘法累加)。工作量:要做 `N` 道菜,每道菜都需要 `N` 步基础操作。总工作量大约是 `N * N = N^2`。 后果:如果 `N = 1024`,工作量就是 `1024 * 1024 ≈ 100万` 步。如果 `N = 4096`,工作量就飙升到约 `1600万` 步。对于需要实时响应的电脑或手机来说,这个速度太慢了,简直是灾难! FFT的诞生,就是为了解决这个效率问题。它不是一种新的变换,而是一种计算DFT的、极其聪明的“烹饪流程”或“快捷算法”。
核心知识一:FFT 不是什么?
在深入了解之前,我们必须明确:FFT 不是一种新的变换:它和DFT要到达的目的地是完全一样的。FFT 的计算结果与 DFT 完全相同:(在忽略计算机浮点误差的前提下)你用FFT算出的频谱,和你用DFT“硬算”出来的频谱,每一个数字都一模一样。FFT 是一种算法:它是一种实现DFT计算的快速方法。
比喻:DFT是“从北京开车到上海”这个目标。直接计算DFT是“开着拖拉机走国道”,虽然能到,但慢得要死。FFT是“坐着高铁走京沪线”,同样能到,但速度快了成百上千倍。
核心知识二:FFT的“独门秘籍” —— 分而治之 (Divide and Conquer)
FFT的全部魔力都来源于这个简单的策略。这位聪明的FFT厨师发现,这份1024道菜的大订单里,有很多菜的“半成品”是可以共用的!
第一步:拆分任务
FFT厨师拿到1024个输入点 `x[n]` 的任务后,他没有直接开干,而是做了一个天才的决定:把原始序列,按照索引的奇偶,拆分成两个更小的序列。
偶数序列 `x_even`: `x[0], x[2], x[4], ...` (长度为 N/2 = 512)
奇数序列 `x_odd`**: `x[1], x[3], x[5], ...` (长度为 N/2 = 512)
现在,他把一个大的1024点的DFT任务,变成了两个小的512点的DFT任务。
第二步:递归拆分
这位厨师是个递归思想的狂热爱好者。他会对这两个512点的任务,再次使用同样的策略:
512点偶数序列 → 拆分成256点的“偶中偶”和256点的“偶中奇”。
512点奇数序列 → 拆分成256点的“奇中偶”和256点的“奇中奇”。
他会一直这样拆分下去,直到任务变得极其简单为止。最简单的任务是什么?2个点的DFT!这个计算简单到只需要一次加法和一次减法。
第三步:合并结果(这步是魔法的关键!)
当所有小任务都完成后,就需要把这些“半成品”巧妙地组合起来,得到最终的大订单结果。FFT厨师发现了一个惊人的数学规律:一个 N 点的DFT结果,可以由其内部两个 N/2 点的DFT结果,通过非常简单的加减法和一次乘法组合而成。
这个组合公式是FFT的核心:
`X[k] = E[k] + W * O[k]`
`X[k + N/2] = E[k] - W * O[k]`
让我们来解读这个“魔法食谱”:`X[k]` 和 `X[k + N/2]`: 我们最终想要的1024点DFT结果中的两个点。
`E[k]` 和 `O[k]`: 分别是那两个512点DFT(偶数和奇数序列)的结果。
`W`: 这就是所谓的“旋转因子” (Twiddle Factor)。它是一个复数,可以看作是一种“相位胶水”,用来把奇数部分的结果“旋转”到一个正确的角度,再和偶数部分的结果合并。最神奇的地方:你发现了吗?我们只计算了一次 `E[k]` 和一次 `W * O[k]`,通过一次加法和一次减法,就同时得到了两个最终结果 `X[k]` 和 `X[k + N/2]`!这就是计算量减半的秘密所在!我们重复利用了中间计算结果。
核心知识三:视觉化理解 —— 蝶形图 (Butterfly Diagram)
这个巧妙的合并过程,可以用一张图来表示,因为它的形状酷似一只蝴蝶,所以被称为蝶形图。

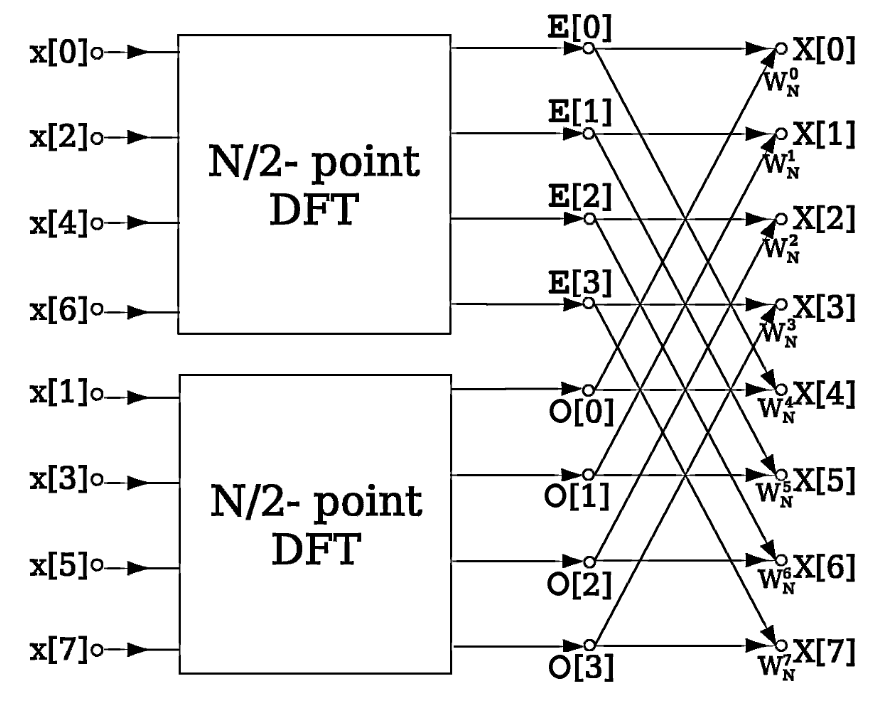
输入端 (左侧):`E[k]` 和 `O[k]` (两个半成品)。
输出端 (右侧):`X[k]` 和 `X[k + N/2]` (两道最终的菜)。
中间的连线:上路直接通过。下路在通过前,需要乘以那个“旋转因子” `W`。在输出端,上下两路汇合,进行一次加法(得到 `X[k]`)和一次减法(得到 `X[k+N/2]`)。 整个FFT的计算过程,就是由无数个这样的小“蝴蝶”逐级构成的。从最小的2点DFT开始,像搭积木一样,一级一级地合并,最终构建出完整的N点DFT结果。
核心知识四:FFT的“游戏规则” —— N必须是2的幂
因为FFT的核心是“不断地对半分”,所以这个算法最自然、最高效的形式要求输入信号的长度 `N` 必须是2的幂,比如 64, 128, 256, 1024, 4096...
问:如果我的信号长度不是2的幂,比如是1000个点,怎么办?
答:补零 (Zero-padding)!这是非常常见的工程实践。我们会在这1000个点的信号末尾,补上24个零,把它凑成1024个点。这样做不仅能让FFT算法顺利运行,还有一个额外的好处:它相当于在频域上进行了插值,会让你的频谱曲线看起来更平滑、更精细。
核心知识五:FFT的巨大影响力
FFT将DFT的计算复杂度从 `O(N^2)` 降到了 `O(N log N)`。这是什么概念?
| 点数 N | DFT (N^2) | FFT (N log N) | 速度提升倍数 |
| 1024 | ~ 1,000,000 | ~ 10,000 | ~ 100倍 |
| 4096 | ~ 16,000,000 | ~ 50,000 | ~ 320倍 |
| 1,048,576 | ~ 1,000,000,000,000 | ~ 20,000,000 | ~ 50,000倍 |
这种指数级的提升,使得许多依赖于傅里叶分析的现代技术从“理论上可行”变成了“实践中可用”。
实际应用例子:4G/5G通信中的OFDM技术。为了在有限的无线频谱上传输海量数据,4G和5G使用了OFDM技术。它把高速的数据流,分解成数千个并行的低速子数据流,每个子数据流被调制到一个独立的、靠得很近的子载波频率上。在手机的发射端,需要把这几千路信号合成一个复杂的时域波形。这个过程,在数学上就是一个逆FFT (IFFT)。在接收端(比如你的手机),需要从接收到的复杂波形中,把这几千路信号精确地分离出来。这个过程,就是一个FFT。没有FFT的惊人速度,你的手机根本不可能实时地完成如此复杂的调制解调任务,4G/5G也就无法实现。
