引言:从“电影”到“翻页动画书”的艺术
想象一下,你是一位伟大的动画导演,你刚刚用摄像机拍了一段连续流畅的电影,记录了一只小鸟飞翔的优美轨迹。这部电影就是我们的连续时间信号 `x(t)`。 现在,你需要把这部电影制作成一本给孩子看的翻页动画书。这本动画书就是离散时间信号 `x[n]`。 采样 (Sampling),就是你决定“多久拍一张照片”的这个过程。
问题:我应该拍得多快?拍得太慢,小鸟的动作就会变得卡顿、不连贯,甚至可能完全误解它的飞行路径。拍得太快,书会变得超级厚,浪费纸张和存储空间。
采样的核心:找到一个“刚刚好”的拍照速度,既能完美地、无损地记录下小鸟的所有飞行动作,又不会造成浪费。
香农采样定理,就是揭示这个“刚刚好”速度的惊天秘密的“导演手册”。
核心知识一:采样的数学本质 —— 冲激串调制
如何“拍照”?
他没有用“记录”这个词,而是把采样看作是原始的连续信号 `x(t)` 与一个周期性的冲激串 `p(t)`相乘。
冲激串 `p(t)`: `p(t) = ∑ δ(t - nT)` (从 n=-∞ 到 +∞)
比喻:它就像一个无限快的、周期性的闪光灯。每隔 `T` 秒,它就“咔嚓”闪一下。`T` 就是我们的采样周期。
采样后的信号 `x_p(t)`:`x_p(t) = x(t) * p(t) = ∑ x(nT)δ(t - nT)`
比喻:当这个闪光灯闪烁时,它只会“照亮”电影 `x(t)` 在那一瞬间 `nT` 的画面 `x(nT)`。在其他没有闪光的时刻,一切都是黑暗的(值为0)。所以,`x_p(t)` 是一串带权重的冲激,它在时域上仍然是一个连续时间信号(虽然只在离散点上有值),但它完美地保留了我们在每个采样时刻的样本值。从 `x_p(t)` 到 `x[n]`:我们把第 `n` 个冲激的权重 `x(nT)` 拿出来,就得到了我们的离散序列 `x[n]`。
为什么这个模型如此重要?
因为它把采样从一个看似简单的“记录”操作,变成了一个信号调制的数学模型。这使得我们可以用强大的傅里-叶变换来分析它在频域中到底发生了什么!
核心知识二:采样在频域的“大揭秘”
这是本章的灵魂!当我们在时域把信号乘以一个冲激串时,在频域会发生什么? 根据卷积定理,我们知道: 时域相乘 ↔ 频域卷积。所以,采样后信号的频谱 `X_p(jω)` 等于原始信号的频谱 `X(jω)` 与冲激串的频谱 `P(jω)` 的卷积。
1. 原始信号的频谱 `X(jω)`:
比喻:这是我们原始电影 `x(t)` 的“配方单”。假设小鸟飞得不快,所以它的配方主要集中在低频区域(比如 `-ω_M` 到 `+ω_M` 之间),我们称之为带限信号。
2. 冲激串的频谱 `P(jω)`:
一个时域的周期冲激串,其傅里-叶变换仍然是一个频域的周期冲激串!
`P(jω) = (2π/T) * ∑ δ(ω - kω_s)` ,
`ω_s = 2π/T`,这就是大名鼎鼎的采样频率(角频率形式)。
比喻:时域的周期性“闪光灯”,在频域变成了一排周期性的“镜子”,每面镜子间隔 `ω_s`。
3. 卷积结果 `X_p(jω)`:
`X_p(jω) = (1/T) * ∑ X(j(ω - kω_s))`
惊人的结果:一个信号与一个冲激串卷积,其效果就是把这个信号的频谱以采样频率 `ω_s` 为周期,进行无限的、周期的复制粘贴!
比喻:原始的“配方单” `X(jω)`,被频域的那一排“镜子” `P(jω)` 反复映射,形成了一长串一模一样的、等间距的频谱副本。这就是采样的本质:时域的离散化,导致了频域的周期化。
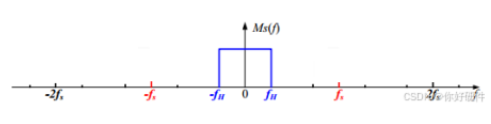
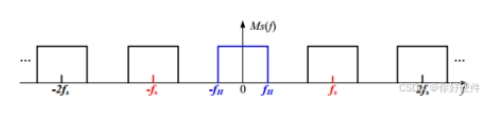
核心知识三:奈奎斯特-香农采样定理 (The Nyquist-Shannon Sampling Theorem)
现在,我们面临一个关键问题:如何从这堆无限复制的频谱中,完美地恢复出原始的那个频谱? 看上图,答案显而易见:只要这些频谱副本彼此之间没有发生重叠,我们就可以用一个理想低通滤波器(像一把“剪刀”),把 `ω=0` 附近的那个原始副本完整地裁剪出来,从而完美恢复原始信号。
什么时候会发生重叠?
当采样频率 `ω_s` 太小时,频谱副本之间的间距就太近了。原始频谱的宽度是 `2ω_M`。如果 `ω_s < 2ω_M`,那么一个频谱的“尾巴”就会和下一个频谱的“脑袋”混叠在一起。
混叠 (Aliasing): 一旦发生重叠,高频成分就会“伪装”成低频成分,信息就被永久性地破坏了,再也无法分清。著名的比喻:车轮效应。在电影中,当车轮转速很快时,如果你摄像机的“采样率”(帧率)不够高,你会看到车轮在缓慢地倒转。这就是一个高频的旋转运动,因为采样不足,被“混叠”成了一个低频的倒转运动。
采样定理的正式声明: 一个带限信号(其最高频率为 `ω_M`),如果其采样频率 `ω_s` 大于其最高频率的两倍(`ω_s > 2ω_M`),那么这个信号就可以从其样本值中被完美地、无失真地恢复出来。
`2ω_M` 被称为奈奎斯特频率 (Nyquist Rate)。你必须以比它更快的速度去采样。这个定理是整个数字信息时代的基石!它告诉我们,可以用有限的数字,来完美地代表一个连续的世界。
核心知识四:重建 —— 从“翻页书”回到“电影”
如果我们满足了采样定理,如何操作才能把离散的样本 `x[n]` 变回连续的电影 `x(t)` 呢?
数学操作:将采样后的信号 `x_p(t)`(那串带权重的冲激)通过一个理想低通滤波器。
滤波器的设置:
增益:`T`
截止频率 `ω_c`:介于 `ω_M` 和 `ω_s - ω_M` 之间(比如 `ω_s/2`)。
时域的理解:理想低通滤波器的冲激响应是一个 `sinc` 函数。 所以,重建过程等价于在每个采样点 `nT` 的位置,放上一个高度为 `x[n]` 的 `sinc` 函数,然后把所有这些 `sinc` 函数叠加起来。 `x(t) = ∑ x[n] * sinc((t-nT)/T)`
比喻:这就像一个极其高明的“插画师”。他看着你翻页动画书上的每一个离散的画面点 `x[n]`,然后用一支神奇的 `sinc` 画笔,在每个点周围画出一个优美的、会影响到周围所有时刻的波纹。当所有这些波纹叠加在一起时,就奇迹般地重构出了小鸟飞行的那条连续、平滑的轨迹!
